2025年05月04日成考高起点每日一练《数学(理)》

2025年成考高起点每日一练《数学(理)》5月4日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知向量a=(3,4),向量 b=(0,-2),则cos的值为（）

• A：
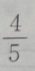
• B：
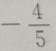
• C：
• D：

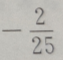
答 案：B

解 析：求cos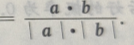可直接用公式cos a·b=(3,4)·(0,-2)=3×0+4×(-2)=8,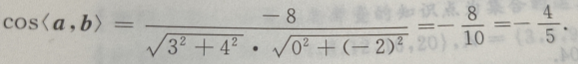  

2、函数的定义域为（）。

• A：R
• B：{1}
• C：{x||x|≤1)
• D：{x||x|≥1}

答 案：A

解 析：本题主要考查的知识点为函数的定义域. 对于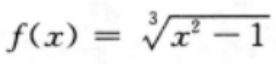，奇次根号下无要求，故函数的定义域为R

3、若函数f（x）是奇函数，则函数的奇偶性是（）。

• A：奇函数
• B：偶函数
• C：非奇非偶函数
• D：即是奇函数，又是偶函数

答 案：A

解 析：∵f(x)是奇函数 ∴f(-x)=-f(x) ∵F(x)=f(x)·(-cosx)=-f(x)cosx ∴F(-x)=-f(-x)cos(-x)= f(x)cosx =-F(x) 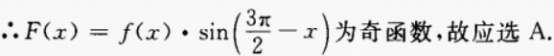注：由此可知，奇函数×偶函数为奇函数；奇函数×奇函数为偶函数；偶函数×偶函数为偶函数。

4、（）。

• A：
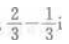
• B：
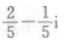
• C：
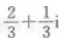
• D：

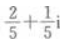
答 案：D

解 析：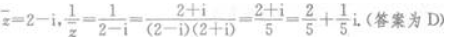

主观题

1、已知a^m=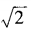，an=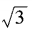，求a3^n-4m的值。  

答 案：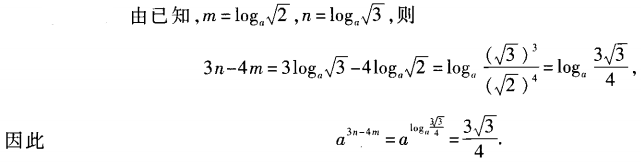

2、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．

答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得当时，f'(x)时，f'(x)＞O.故f(x）在区间单调递减，在区间单调递增．因此f(x）在时取得极小值

3、某工厂每月生产x台游戏机的收入为R(x)=+130x-206(百元)，成本函数为C(x)=50x+100(百元)，当每月生产多少台时,获利润最大?最大利润为多少?  

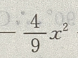答 案：利润 =收入-成本， L(x)=R(x)-C(x)=+130x-206-(50x+100)=+80x-306 法一：用二次函数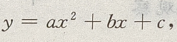当a<0时有最大值 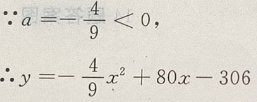是开口向下的抛物线，有最大值 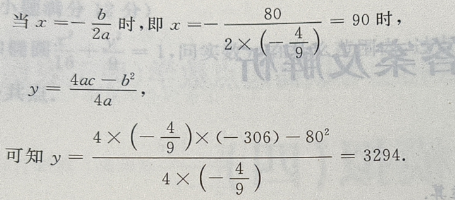法二：用导数来求解 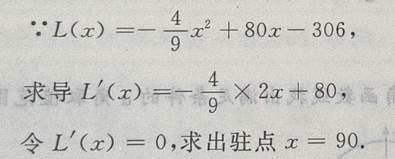因为x=90是函数在定义域内唯一驻点 所以x=90是函数的极大值点，也是函数的最大值点，其最大值为L（90）=3294  

4、已知lg2=a，lg3=b，求lg0.15关于a，b的表达式。  

答 案：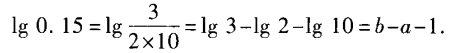

填空题

1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。  

答 案：85  

解 析：本题主要考查的知识点为中位数. 将成绩按由小到大排列：63，77，79，81，85，88，89，94，99.因此中位数为85。

2、已知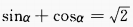，则=______。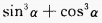  

答 案：

解 析：