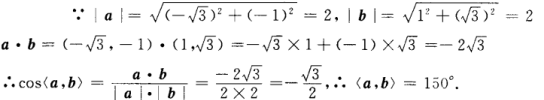2025年05月02日成考高起点每日一练《数学(理)》

2025年成考高起点每日一练《数学(理)》5月2日专为备考2025年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、设二次函数f(x)=x²+px+q的图象经过点(1,一4)且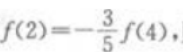则该二次函数的最小值为（）。

• A：－6
• B：－4
• C：0
• D：10

答 案：B

解 析：

2、函数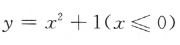的反函数是（）

• A：
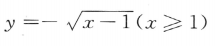
• B：
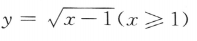
• C：
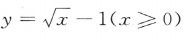
• D：

答 案：A

解 析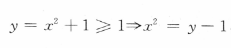：，由于x≤0，故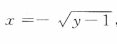把x与y互换，得所求反函数为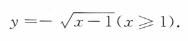

3、抛物线y＝ax²（a＜0）的焦点坐标是（）。

• A：
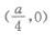
• B：
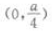
• C：
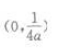
• D：

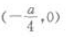
答 案：C

解 析：

4、下列各式中，不成立的是（）。

• A：
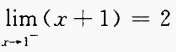
• B：
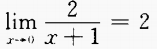
• C：
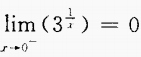
• D：

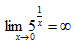
答 案：D

解 析：可用排除法，A、B、C均成立。

主观题

1、已知数列的前n项和 求证：是等差数列，并求公差和首项。  

答 案：  

2、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得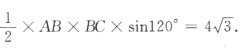所以AB =4.因此所以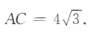

3、如图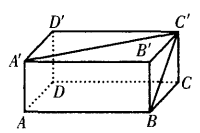，已知长方体的长和宽都是4cm，高是2cm。求 （1）BC和A’C’所成的角是多少度?
（2）A’B’和DD’的距离是多少?

答 案：（1）在长方体中BC和A’C’不在同一个平面内 所以BC和A’C’是异面直线 ∵在长方体中BC//B’C’ ∴∠A’C’B’是异面直线BC和A’C’所成的角
∵A’C’B’=45°
异面直线BC和A’C’所成的角是45°
（2）A’B’和DD’是异面直线
∵A’D’⊥A’B’ A’D’⊥DD’
∴A’D’的长即为异面直线A’B’和DD’的距离
∵A’D’=4
∴A’B’和DD’间的距离为4cm。

4、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得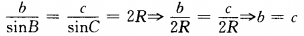

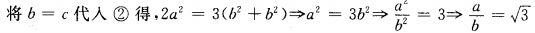
∴a：b=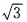：1
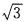于是a：b：c=：1：1。  

填空题

1、化简sin（x+y）-2cosxsiny=______.  

答 案：sin（x-y）

解 析：原式=sinxcosy+cosxsiny-2cosxsiny=sinxcosy-cosxsiny=sin（x-y）

2、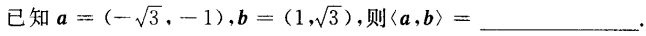  

答 案：；150°

解 析：